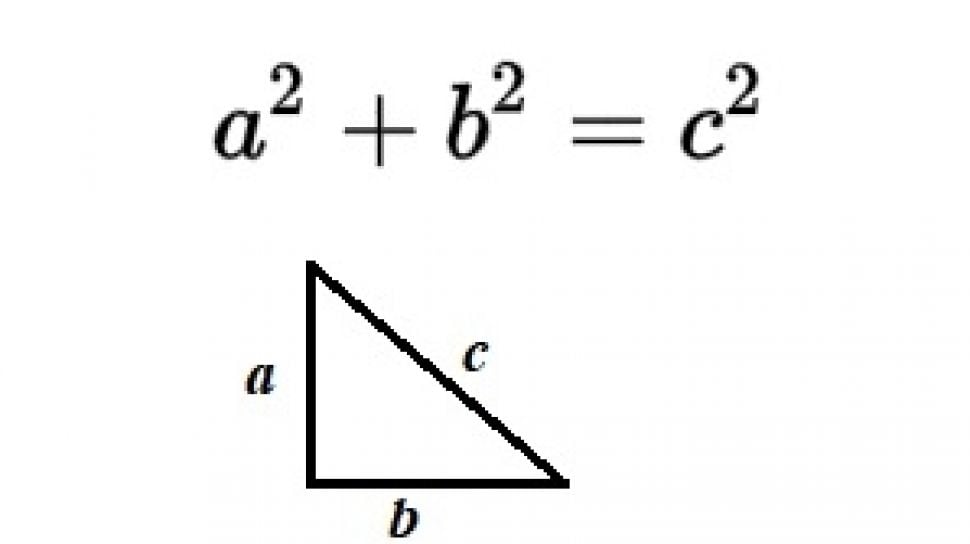
Belajar matematika tentunya kita juga akan belajar rumus, banyak sekali rumus yang dapat kita pelajari di Pelajaran matematika. Salah satu rumus yang cukup popular adalah rumus Pythagoras. Pada rumus Pythagoras kita akan belajar cara menghitung sisi dari sebuah segitiga siku-siku. Maka berikut ini rumus dan contoh soal menggunakan rumus Pythagoras adalah:
- Sejarah Teorema Pythagoras
Teorema Pythagoras pertama kali ditemukan oleh bangsa Yunani, yakni Pythagoras. Namun ternyata teoram Pythagoras ini telah digunakan sejak 1900-1600 SM oleh penduduk Cina dan Babilonia.
Dan lebih jauh juga pada tahun 800 dan 400 SM di kitab Baudhayana Sulba Sutra di India. Hingga akhirnya nama Pythagoras diambil sebagai nama teori ini dikarenakan Pythagoras yang dapat membuktikan rumus ini secara matematis.
- Materi Teorema Pythagoras
Teorema Pythagoras ini Dimana car akita untuk mendapatkan dan menghitung sisi segitiga siku-siku. Segitiga siku-siku memiliki tiga buah sisi yakni alas, tinggi dan sisi miring atau hipotenusa. Bunyi dari dalil teorema Pythagoras adalah segitiga siku-siku dikuadratkan dari sisi miring sama dengan jumlah kuadrat dari sisi-sisi lainnya.
Maka dengan begitu ketiga sisi itu saling terikat. Ada dua hal wajib yang harus dimiliki yakni, hanya berlaku pada segitiga siku-siku, dan harus diketahui minimal dua sisi terlebih dahulu untuk menentukan sisi lainnya. Maka tujuan dari segitiga ini adalah untuk mengetahui Panjang dari salah satu sisi dari segitiga.
- Rumus Teorema Pythagoras
Berdasarkan bunyi dari teorema Pythagoras menyatakan bahwa segitiga siku-siku dengan penanda a,b,c. sebagai contoh sebuah segitiga siku-siku dengan alas a, tinggi b dan sisi miring atau hipotenusa c. Maka jumlah kuadrat dari sisi c sama dengan jumlah kuadrat dari sisi a dan b.
Rumus Teorema Pythagoras
- Untuk mencari sisi miring dari segitiga siku-siku:
c2 = a2 + b2
- Untuk mencari sisi alas dari segitiga siku-siku:
b2 = c2 – a2
- Untuk mencari sisi tinggi dari segitiga siku-siku:
a2 = c2 – a2
Namun ada cara lainnya untuk menemukan sisi dari segitiga siku-siku. Cara itu adalah dengan cara menghafalkan triple Pythagoras. Hal ini dikarenakan ukuran pasti dari sisi-sisi segitiga Pythagoras. Maka berikut ini angka-angka yang disebut dengan triple Pythagoras.
- 3, 4 dan 5
- 6, 8 dan 10
- 5, 12 dan 13
- 7, 24 dan 25
- 8, 15 dan 17
- 9, 12 dan 15
- 10, 24 dan 26
- Dan selanjutnya
Maka maksud dari deret tersebut yakni jika segitiga siku-siku memliki tinggi 5 cm, dan alas 12 cm maka sisi kemiringannya adalah 13 cm. Dengan kita menghapalkan deret triple Pythagoras ini maka tentunya akan memudahkan dan mempersingkat waktu kita dalam mengerjakan sebuah soal.
- Contoh Soal Rumus Pythagoras
Diketahui sebuah segitiga siku-siku mempunyai tinggi 8 cm dengan alas 15 cm. Maka tentukan sisi kemiringan dari segitiga siku-siku tersebut adalah.
Jawab:
a = 15
b = 8
c = ?
c2 = a2 + b2
c2 = 152 + 82
c2 = 225 + 64
c = 289
c = 17
maka sisi miring segitiganya adalah 17 cm.
- Diketahui sebuah segitiga siku-siku mempunyai tinggi 9 cm dan sisi kemiringannya 15 cm. Maka tentukan sisi alas dari segitiga siku-siku tersebut adalah
Jawab
b = 9
c = 15
a = ?
a2 = c2 – b2
a2 = 152 – 92
a2 = 225 – 81
a = 144
a = 12
maka sisi alas segitiganya adalah 12 cm.